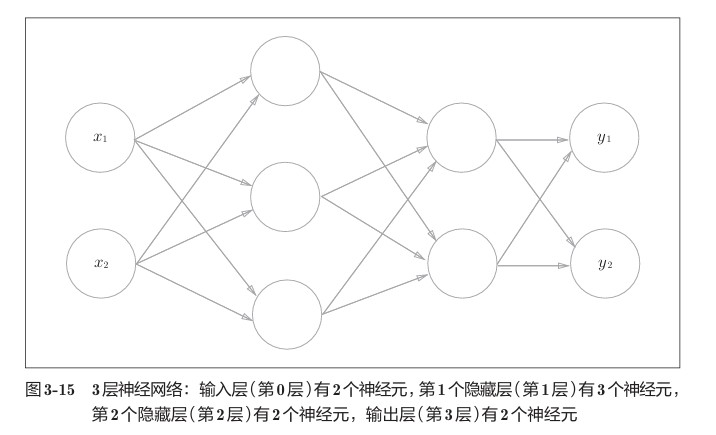
以3层神经网络为对象,实现从输入到输出的(前向)处理。巧妙地使用NumPy数组,可以用很少的代码完成神经网络的前向处理。
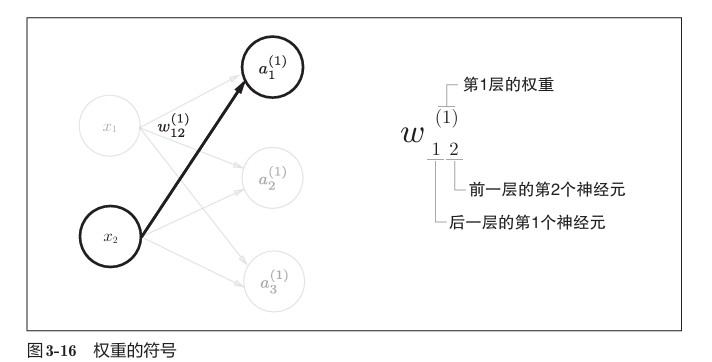
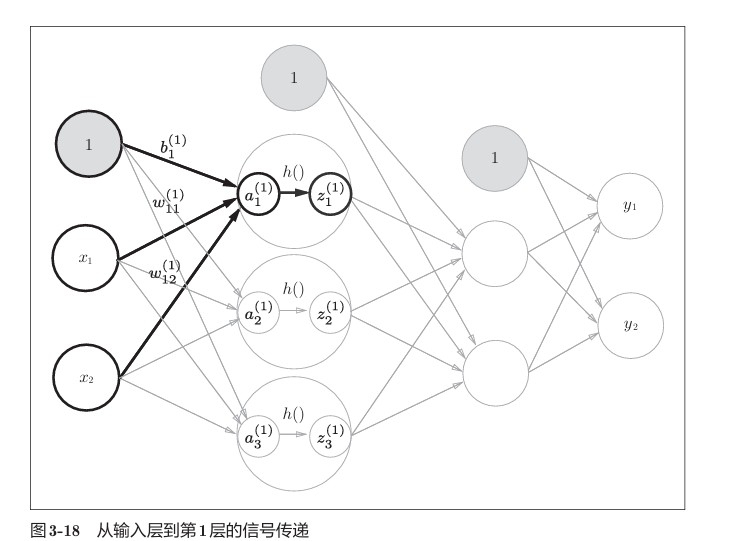
先从定义符号开始。如图所示,权重和隐藏层的神经元的右上角有一个“(1)”,它表示权重和神经元的层号(即第1层的权重、第1层的神经元)。此外,权重的右下角有两个数字,它们是后一层的神经元和前一层的神经元的索引号。比如,表示前一层的第2个神经元x2 到后一层的第1个神经元的权重。权重右下角按照“后一层的索引号、前一层的索引号”的顺序排列。
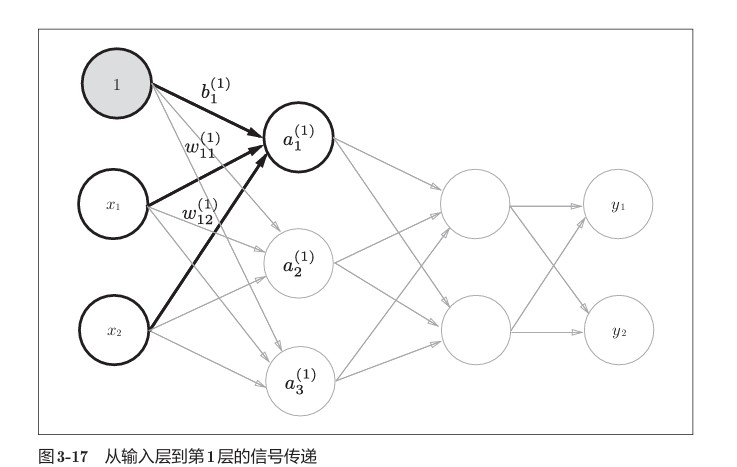
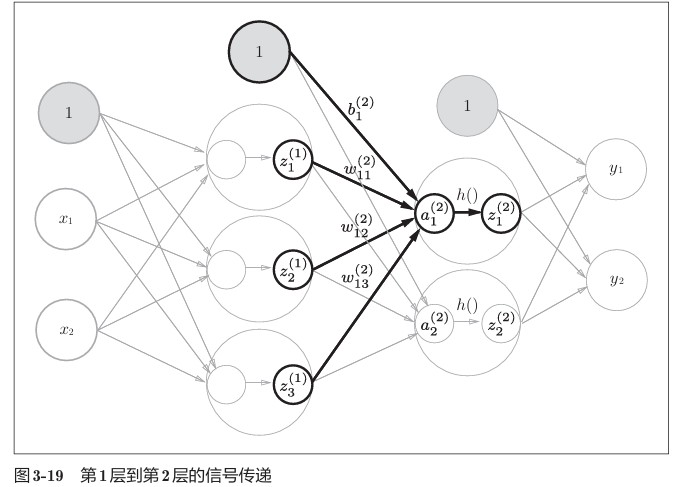
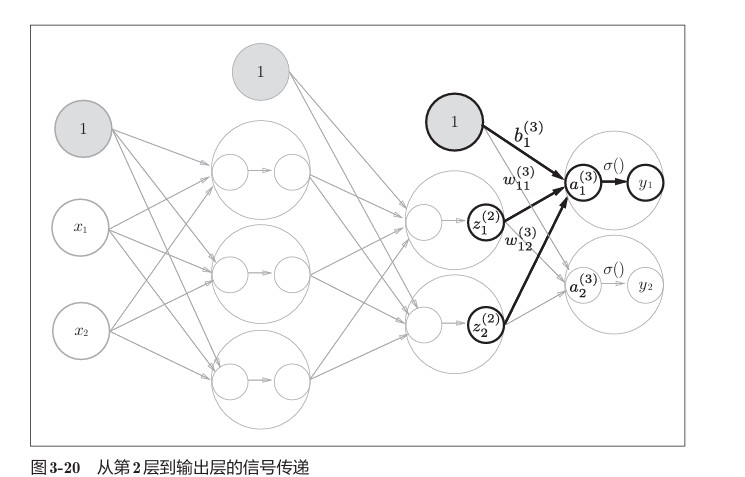
各层间信号传递的实现
def init_network():
network = {}
network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
network['b1'] = np.array([0.1, 0.2, 0.3])
network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
network['b2'] = np.array([0.1, 0.2])
network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
network['b3'] = np.array([0.1, 0.2])
return network
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identity_function(a3)
return y
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y) # [ 0.31682708 0.69627909]这里定义了init_network()和forward()函数。init_network()函数会进行权重和偏置的初始化,并将它们保存在字典变量network中。这个字典变量network中保存了每一层所需的参数(权重和偏置)。forward()函数中则封装了将输入信号转换为输出信号的处理过程。
另外,这里出现了forward(前向)一词,它表示的是从输入到输出方向的传递处理。后面在进行神经网络的训练时,我们将介绍后向(backward,从输出到输入方向)的处理。
至此,神经网络的前向处理的实现就完成了。通过巧妙地使用NumPy多维数组,我们高效地实现了神经网络。
输出层的设计
神经网络可以用在分类问题和回归问题上,不过需要根据情况改变输出层的激活函数。一般而言,回归问题用恒等函数,分类问题用softmax函数。
恒等函数会将输入按原样输出,对于输入的信息,不加以任何改动地直接输出。
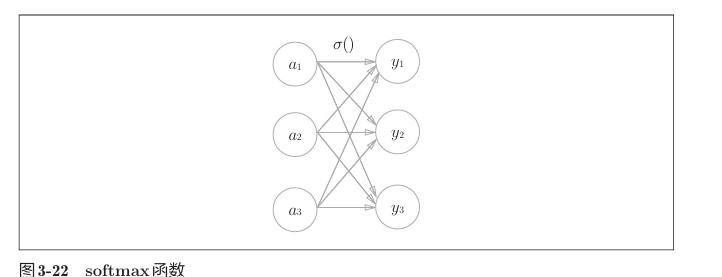
分类问题中使用的softmax函数可以用下面的式表示。
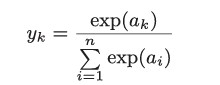
exp(x)是表示ex的指数函数(e是纳皮尔常数2.7182…)。 假设输出层共有n个神经元,计算第k个神经元的输出yk。
softmax函数的分子是输入信号ak的指数函数,分母是所有输入信号的指数函数的和。
def softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y实现softmax函数时的注意事项
softmax函数的实现中要进行指数函数的运算,但是此时指数函数的值很容易变得非常大,容易溢出。为了防止溢出,一般会使用输入信号中的最大值。
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c) # 溢出对策
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return ysoftmax函数的特征
输出总和为1是softmax函数的一个重要性质。根据此性质,可以把softmax函数的输出解释为“概率”。
也就是说,通过使用softmax函数,我们可以用概率的(统计的)方法处理问题。
一般而言,神经网络只把输出值最大的神经元所对应的类别作为识别结果。并且,即便使用softmax函数,输出值最大的神经元的位置也不会变。因此,神经网络在进行分类时,输出层的softmax函数可以省略。在实际的问题中,由于指数函数的运算需要一定的计算机运算量,因此输出层的softmax函数一般会被省略。
求解机器学习问题的步骤可以分为“学习”A 和“推理”两个阶段。首先,在学习阶段进行模型的学习B,然后,在推理阶段,用学到的模型对未知的数据进行推理(分类)。如前所述,推理阶段一般会省略输出层的softmax函数。在输出层使用softmax函数是因为它和神经网络的学习有关系
输出层的神经元数量
输出层的神经元数量需要根据待解决的问题来决定。对于分类问题,输出层的神经元数量一般设定为类别的数量。
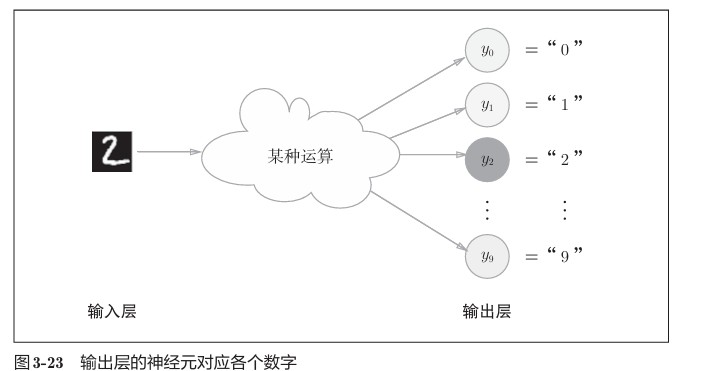
如图所示,在这个例子中,输出层的神经元从上往下依次对应数字0, 1, …, 9。此外,图中输出层的神经元的值用不同的灰度表示。这个例子中神经元y2颜色最深,输出的值最大。这表明这个神经网络预测的是y2对应的类别,也就是“2”。