神经网络的一个重要性质是它可以自动地从数据中学习到合适的权重参数。

神经网络的例子

用图来表示神经网络的话，如图1所示

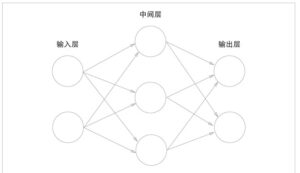
把最左边的一列称为输入层，最右边的一列称为输出层，中间的一列称为中间层。中间层有时也称为隐藏层。“隐藏”一词的意思是，隐藏层的神经元（和输入层、输出层不同）肉眼看不见。

图1中的网络一共由3层神经元构成，但实质上只有2层神经元有权重，因此将其称为“2层网络”。请注意，有的书也会根据构成网络的层数，把图1的网络称为“3层网络”。

激活函数

神经网络中用sigmoid函数作为激活函数，进行信号的转换，转换后的信号被传送给下一个神经元。

sigmoid函数的python实现

def sigmoid(x):
return 1 / (1 + np.exp(-x))

神经网络的激活函数必须使用非线性函数。换句话说，激活函数不能使用线性函数。为什么不能使用线性函数呢？因为使用线性函数的话，加深神经网络的层数就没有意义了。

ReLU函数

Rectified Linear Unit：ReLU函数在输入大于0时，直接输出该值；在输入小于等于0时，输出0。

def relu(x):
return np.maximum(0, x)

 

多维数组的运算

如果掌握了NumPy多维数组的运算，就可以高效地实现神经网络。

多维数组就是“数字的集合”，数字排成一列的集合、排成长方形的集合、排成三维状或者（更加一般化的）N维状的集合都称为多维数
组。二维数组也称为矩阵（matrix）。数组的横向排列称为行（row），纵向排列称为列（column）。

矩阵乘法

矩阵的乘积是通过左边矩阵的行（横向）和右边矩阵的列（纵向）以对应元素的方式相乘后再求和而得到的。并且，运算的结果保存为新的多维数组的元素。比如，A的第1行和B的第1列的乘积结果是新数组的第1行第1列的元素，A的第2行和B的第1列的结果是新数组的第2行第1列的元素。

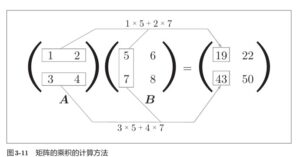
A = np.array([[1,2], [3,4]])

A.shape

B = np.array([[5,6], [7,8]])

B.shape

np.dot(A, B)

要注意的是，np.dot(A, B)和np.dot(B, A)的值可能不一样。和一般的运算（+或*等）不同，矩阵的乘积运算中，操作数（A、B）的顺序不同，结果也会不同。