神经网络概说2025/05/12

在人工智能的世界里，神经网络无疑是最炙手可热的技术之一。​无论是图像识别、自然语言处理，还是自动驾驶，神经网络都扮演着至关重要的角色。​然而，对于初学者来说，神经网络可能显得既神秘又复杂。​本文将以通俗易懂的方式，带你走进神经网络的世界，揭开其神秘的面纱。​

一、什么是神经网络？

神经网络，顾名思义，是受人脑神经系统启发而设计的计算模型。​它由大量的“神经元”组成，这些神经元通过连接权重相互连接，形成一个复杂的网络结构。​神经网络的强大之处在于，它可以通过学习大量的数据，自动调整连接权重，从而实现对复杂模式的识别和预测。​

神经网络的例子

用图来表示神经网络的话，如图1所示

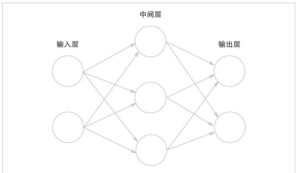
把最左边的一列称为输入层，最右边的一列称为输出层，中间的一列称为中间层。中间层有时也称为隐藏层。“隐藏”一词的意思是，隐藏层的神经元（和输入层、输出层不同）肉眼看不见。

图1中的网络一共由3层神经元构成，但实质上只有2层神经元有权重，因此将其称为“2层网络”。请注意，有的书也会根据构成网络的层数，把图1的网络称为“3层网络”。

二、神经网络的基本结构

一个典型的神经网络通常包括以下几层：​

• 输入层（Input Layer）：​负责接收外部输入数据。​
• 隐藏层（Hidden Layer）：​位于输入层和输出层之间，负责对输入数据进行特征提取和转换。​
• 输出层（Output Layer）：​将隐藏层提取的特征转换为最终的输出结果。​

需要注意的是，虽然隐藏层被称为“隐藏”，但它们在整个网络中起着至关重要的作用。​它们通过非线性变换，使神经网络具备了处理复杂问题的能力。​

三、激活函数：神经网络的非线性引擎

在神经网络中，激活函数的作用是将神经元的输入信号进行非线性变换，从而引入非线性因素，使网络能够处理更复杂的任务。​

1. Sigmoid函数

Sigmoid函数是最早被广泛使用的激活函数之一，其数学表达式为：​

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

Sigmoid函数的输出范围在0到1之间，适合处理概率问题。​然而，它存在梯度消失的问题，尤其是在深层网络中，可能导致训练困难。​

2. ReLU函数

ReLU（Rectified Linear Unit）函数是目前最常用的激活函数之一，其定义为：​

def relu(x):
    return np.maximum(0, x)

ReLU函数在输入大于0时，直接输出该值；在输入小于等于0时，输出0。​它的优点是计算简单，能够有效缓解梯度消失问题。​

四、矩阵运算：神经网络的数学基础

神经网络的计算本质上是大量的矩阵运算。​通过矩阵乘法，可以高效地实现神经元之间的连接和信号传递。​

矩阵的乘积是通过左边矩阵的行（横向）和右边矩阵的列（纵向）以对应元素的方式相乘后再求和而得到的。并且，运算的结果保存为新的多维数组的元素。比如，A的第1行和B的第1列的乘积结果是新数组的第1行第1列的元素，A的第2行和B的第1列的结果是新数组的第2行第1列的元素。

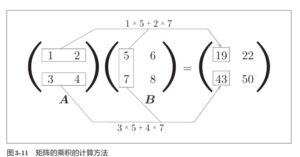
例如，给定两个矩阵A和B，它们的乘积可以通过NumPy中的 dot 函数计算：​

A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
np.dot(A, B)

需要注意的是，矩阵乘法不满足交换律，即 np.dot(A, B) 和 np.dot(B, A) 的结果可能不同。​

五、学习神经网络的建议

对于初学者来说，掌握神经网络的基本概念和数学基础是关键。​建议从以下几个方面入手：​

1. 数学基础：​熟悉线性代数、微积分和概率论等数学知识。​
2. 编程能力：​掌握Python编程语言，熟悉NumPy、TensorFlow或PyTorch等深度学习框架。​
3. 实践经验：​通过实际项目，巩固所学知识，提升解决实际问题的能力。​

六、总结

神经网络作为人工智能领域的重要工具，具有强大的学习和表达能力。​通过本文的介绍，希望能够帮助你更好地理解神经网络的基本原理和实现方法。​在未来的学习和实践中，不断探索和深入，将使你在人工智能的道路上越走越远。