神经网络的内积2025/05/12
神经网络的实现涉及复杂的矩阵运算,而 NumPy 作为 Python 中的核心工具,为这些计算提供了高效的支持。本文将详细探讨如何使用 NumPy 矩阵进行内积操作,特别是在神经网络中的应用,并结合示例分析其重要性与效率。
背景介绍:神经网络与矩阵运算
神经网络是一种受人类大脑启发的机器学习模型,广泛应用于图像识别、自然语言处理等领域。其核心是通过多层节点(神经元)处理输入数据,每层节点通过加权连接计算输出。
在实现中,输入、权重和输出通常以矩阵形式表示。例如,一个数据集有 1000 个样本,每个样本有 10 个特征,可用 1000×10 矩阵表示。矩阵运算允许一次性处理所有样本,效率远高于逐个计算。
NumPy 是 Python 的数值计算库,支持多维数组和矩阵运算。其底层使用优化后的 C 代码,提供了向量化操作,显著提升计算速度。在神经网络中,NumPy 常用于数据预处理、权重更新和前向传播计算。
内积操作在神经网络中的角色
内积(点积)是线性代数中的基础操作,对于两个向量 A = [a1, a2, …, an] 和 B = [b1, b2, …, bn],内积为 a1 b1 + a2 b2 + … + an*bn。在神经网络中,这一操作扩展到矩阵间,常用矩阵乘法实现。
例如,前向传播中,输入向量 X 通过权重矩阵 W 计算输出 Y = X * W,其中 * 表示矩阵乘法。这是神经网络每一层计算的核心。
示例分析:X、W 和 Y 的计算
以下是具体示例,展示如何使用 NumPy 进行内积操作: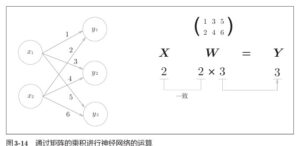
- X = np.array([1, 2]),这是一个 1×2 向量,表示输入特征。
- W = np.array([[1, 3, 5], [2, 4, 6]]),这是一个 2×3 矩阵,表示从输入层到隐藏层的权重。
- 计算 Y = np.dot(X, W),结果为 [5, 11, 17]。
计算过程分解:
- 第一个元素:1 1 + 2 2 = 1 + 4 = 5
- 第二个元素:1 3 + 2 4 = 3 + 8 = 11
- 第三个元素:1 5 + 2 6 = 5 + 12 = 17
X = np.array([1, 2]
W = np.array([[1, 3, 5], [2, 4, 6]])
Y = np.dot(X, W)
print(Y)
这里,X 的列数(2)必须等于 W 的行数(2),否则无法进行矩阵乘法。Y 的形状为 1×3,表示隐藏层三个神经元的输出。
在神经网络中,Y 通常是加权和的中间结果,之后会通过激活函数(如 ReLU 或 sigmoid)引入非线性。但本例仅展示线性变换部分。
维度匹配的必要性
维度匹配是矩阵运算的关键。若 X 和 W 的维度不匹配,NumPy 会抛出错误。例如,若 X 为 [1, 2],W 为 [3, 4, 5],则无法计算,因为 X 的长度(2)不等于 W 的行数(1)。
因此,在实现神经网络时,需始终检查矩阵形状,确保符合运算规则。这一步骤直接影响计算的正确性。
NumPy 的高效性与应用
NumPy 的点积操作(np.dot)通过向量化实现,效率远高于传统 Python 循环。例如,若 W 有 1000 列,计算 Y 仍可一次性完成,特别适合处理大规模数据。
这种效率在深度学习中尤为重要,神经网络常涉及数百万参数和大批量训练数据。NumPy 的优化使其成为教育和小型网络实现的理想工具。
此外,NumPy 支持批处理。例如,若 X 为 [[1, 2], [3, 4]](两个样本),则 np.dot(X, W) 可同时计算两个样本的输出,形状为 2×3。这体现了矩阵运算处理多数据的高效性。
更广阔的上下文:神经网络架构
本例展示单层操作,但在多层神经网络中,这一过程会重复。数据从输入层通过隐藏层到输出层,每层执行矩阵乘法和激活函数。例如,两隐藏层的网络会有 W1(输入到隐藏1)、W2(隐藏1到隐藏2)等。
训练阶段还涉及反向传播调整权重,但那超出了本讨论范围。
实际建议与扩展
在使用 NumPy 实现神经网络时,建议:
- 始终检查矩阵形状,避免维度不匹配。
- 对于大型网络,NumPy 可能因纯 Python 实现而变慢,可考虑 TensorFlow 或 PyTorch,这些框架使用 GPU 加速。
- 理解内积操作有助于调试和优化自定义模型。
总结与展望
内积操作是神经网络实现的基础,NumPy 提供了高效的工具支持。通过示例(如 X = [1, 2],W = [[1, 3, 5], [2, 4, 6]]),我们看到如何计算 Y,并强调维度匹配和计算效率的重要性。
希望本文帮助你更好地理解这一概念,若有更多疑问,欢迎继续讨论!
表格:示例矩阵与计算结果
矩阵/向量形状说明X(2,)输入向量 [1, 2]W(2, 3)权重矩阵 [[1, 3, 5], [2, 4, 6]]Y(3,)输出向量 [5, 11, 17]